ABSTRACT

AIM: Although much has been published on vector-based analysis of astigmatism, the reason why vectors precisely describe astigmatism features, or even changes in its characteristics, has been discussed only on a few articles. Our review intends to highlight the essential features of both methods proposed by Alpins and Thibos.
METHODS: Pubmed was searched for papers in English, containing abstracts, on June 29th 2016 for (astigmatism) AND (vector analysis) AND (Alpins) OR (Thibos), regardless of the date of publication or the study design.
RESULTS: Thirteen papers, out of 228 references, were included in our review. Conclusions: The method proposed by Thibos is suitable whenever an objective description of astigmatism is aimed. However, the method proposed by Alpins may provide detailed information on the assessment of changes in astigmatism.

Keywords: Astigmatism; Refractive error; Cornea;

RESUMO

OBJETIVO: Apesar de a análise vetorial ser amplamente utilizada na literatura, tanto para a descrição de características, como na análise de mudanças no astigmatismo, poucos são os artigos que apresentam a racionalidade do método. Em nossa revisão, apresentamos os pontos mais importantes dos métodos propostos por Alpins e por Thibos.
MÉTODOS: O Pubmed foi pesquisado, em 29 de junho de 2016, para artigos em inglês, com resumo, empregando-se os termos (astigmatism) AND (vector analysis) AND (Alpins) OR (Thibos), independentemente da data ou tipo de publicação.
RESULTADOS: Treze artigos, de 228 referências, foram incluídos em nossa revisão. Conclusões: O método proposto por Thibos é o mais apropriado para descrições objetivas do astigmatismo. O método de Alpins, por outro lado, é o mais indicado para análises referentes a mudanças no astigmatismo.

Palavras-chave: Astigmatismo. Erro refrativo. Córnea.

INTRODUCTION

Vector is a mathematical term defined by magnitude and direction. Astigmatism with cylinder power and axis (refractive), or magnitude and meridian (corneal) fits into such a description.⁽¹⁾ Both astigmatism and astigmatic vectors employ the same units of diopters and degrees; however, astigmatism is a measurable entity, while vectors can only be calculated⁽²⁾ A precise and complete analysis of astigmatism must take its vectorial character into account ⁽³⁾ hence, a vector-based analysis has been extensively used in the literature. ^(2,4,5)

The purpose of the present study was to systematically review the literature to identify the rationale for using vector analysis to study astigmatism. The approach proposed by Alpins and coworkers that described by Thibos et al. were included in our study.

METHODS

This systematic review was structured in accordance with the recommendations of Preferred Reporting Items for Systematic Review and Meta-analysis Protocols (PRISMA-P), 2015.⁽⁵⁾ PubMed/MEDLINE was searched on June 29, 2016, for (astigmatism) AND (vector analysis) AND (Alpins) OR (Thibos). Regardless of the date of publication or the study design, the inclusion criterion was papers containing abstracts that were written in English. This initial search retrieved 228 references. Two review authors (GF, RA) independently screened the records obtained from the electronic search and excluded obviously irrelevant studies. Disagreement was resolved through discussion with a third author (MA). Neither of the review authors was blind to the journal titles, the study authors, or institutions. The flow diagram of the search is shown in Figure 1.

Figure 1. Flow diagram of the search.

RESULTS

We included 13 papers in our review. ^{(1, 2, 3, 4)} These papers conveyed information on the background of vector analysis, ^{(1, 2, 7, 8, 9, 11, 13, 14)} or highlighted its clinical importance. ^{(3, 4, 6, 10, 12)}

DISCUSSION

The method proposed by Thibos et al. represents keratometric astigmatism, including any spherical component, whenever present, in the rectangular vector form as follows: ^{(3, 13, 14)}

• The average keratometric reading (M)

• The meridian of maximum positive power ()

• The vector component along the 0-degree meridian

(J₀) = [−_{(Ksteep − Kflat)}/2] × cos2

• The vector component along the 45-degree meridian

(J₄₅) = [−(_{Ksteep − Kflat})/2] × sin2

• The astigmatic power vector (APV) = (Jo² + J₄₅²)^1/2

• The overall blur vector (Blur) = (M² + J₀² + J₄₅²)^1/2

Alternatively, if a spherocylindrical refractive error is being represented, then, M equals the spherical equivalent, and the keratometric astigmatism is replaced by the refractive cylinder power. It is convenient to geometrically interpret M, J₀, and J₄₅ as coordinates (x, y and z respectively) of a point in a three-dimensional dioptric space. B is the vector drawn from the coordinate origin to the point (M, J₀, J₄₅) and APV is the point (J₀, J₄₅) on the astigmatic plane. ^{(13, 14)} Figure 2 depicts the graphical representation of such vectors.

Figure 2. Representation of vectors, as proposed by Thibos, on a three-dimensional space (APV = astigmatic power vector; B = overall blur vector; J0 = vector component along the 0-degree meridian; J45 = vector component along the 45-degree meridian; M = mean power; x = axis of average keratometric reading or spherical equivalent; y = axis of 0-degree meridian; z = axis of 45-degree meridian; 2α = meridian of maximum positive power). Adapted from: Thibos LN, Wheeler W, Horner D. Power vectors: an application of Fourier analysis to the description and statistical analysis of refractive error. Optom Vis Sci. 1997;74(6):367-75.

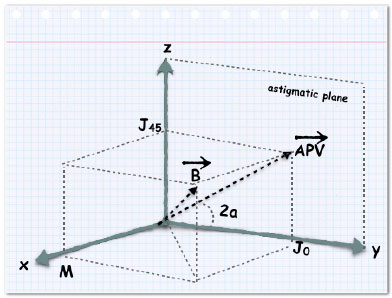
The mathematical concept of orthogonality of vectors simplifies practical problems involving the combination, comparison, and statistical analysis of both spherocylindrical lenses and keratorefractive errors. ⁽¹⁴⁾ In other words, the method proposed by Thibos et al. is perfectly suited for descriptive analysis of astigmatism. ⁽³⁾

The method proposed by Alpins focuses on the evaluation of the surgical correction of astigmatism. It is designed to analyze changes in astigmatism. ⁽⁷⁾ The principle underlying the use of this method relies upon the following three main vectors:

• The intended effect of the astigmatism surgery, i.e., the amount and direction of the treatment required, referred to as the target induced astigmatism vector (TIA).

• The actual surgical effect corresponds to the surgically induced astigmatism vector (SIA).

• The difference vector (DV) measures the amount and the orientation of the treatment required to achieve the initial goal, providing a parameter of astigmatism surgery that effectively measures the error by magnitude and axis. DV is an absolute measure of success and is preferably zero.

Figure 3 shows a graphical calculation of these vectors from a polar astigmatism diagram to a double-angle vector plot.

Figure 3. Graphic vector calculations of astigmatic vectors by Alpins method. 3A) Polar astigmatism diagram: displaying preoperative (α_Pre), postoperative (α_Post), and target (α_T) astigmatism magnitudes at their actual orientation (steep corneal meridian or power axis of negative cylinder). 3B) Double-angle polar astigmatism diagram: astigmatism axis values have been doubled (hence, 2α_Post, 2α_Pre and 2α_T), but the magnitudes of vectors remain unchanged, as required for vector representation. 3C) The dashed lines represent vectors, with arrowheads indicating their orientation (DV = difference vector, SIA = surgically induced vector, TIA = target induced vector). Adapted from: Alpins N, Goggin M. Practical Astigmatism Analysis for Refractive Outcomes in Cataract and Refractive Surgery. Surv Ophthalmol. 2004;49(1):109-22.

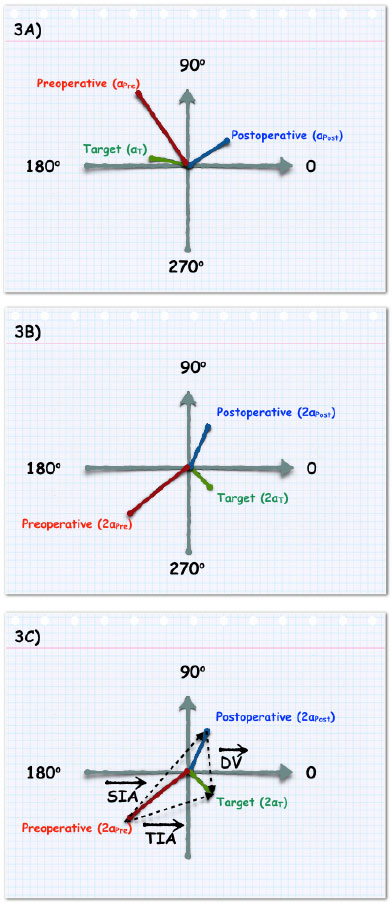
Although the graphic scheme of Alpins's method is simple, sequential trigonometric calculations required to estimate the magnitudes of TIA, SIA, and DV may be troublesome in the clinical setting and is beyond the scope of this review. Copyrighted softwares are currently available to make such calculations easier. ⁽¹¹⁾

Various relationships among such vectors provide objective parameters to evaluate whether the treatment was on-axis or off-axis, whether too much or too little treatment was applied, and the adjustments required in case the same astigmatic correction had to be performed again. ^{(1, 7, 11)} Among these parameters, some broadly used ones are as follows: ^{(1, 11)}

• Correction index (CI): calculated by determining the ratio of SIA to TIA [what the surgery actually induces (actual effect) versus what the surgery was intended to induce (target effect)]. CI is preferably 1.0 (it is >1.0 for overcorrection and <1.0 for undercorrection).

• Magnitude of error (ME): the arithmetic difference between magnitudes of SIA and TIA. The magnitude of error is positive for overcorrection and negative for undercorrection.

• Index of Success (IOS): calculated by dividing DV by TIA (the intended treatment). IOS is a relative measure of success and is preferably 0.

• Coefficient of Adjustment (CA): derived by dividing TIA by SIA, the CI inverse, to adjust future astigmatism treatment (TIA) magnitudes. Its value is preferably 1.0.

In summary, although both methods assess corneal or refractive astigmatism through vector analysis, the method proposed by Thibos is suitable whenever an objective description of astigmatism is desired. However, if any modification in astigmatism is required, then method proposed by Alpins may provide more valuable data.

REFERENCES

1. Alpins N, Goggin M. Practical astigmatism analysis for refractive outcomes in cataract and refractive surgery. Surv Ophthalmol. 2004;49(1):109-22. http://dx.doi.org/10.1016/j.survophthal.2003.10.010

2. Alpins N, Stamatelatos G. Vector analysis applications to photorefractive surgery. Int Opthalmol Clin. 2003;43(3):1-27.

3. Freitas GO, Ambrósio-Jr R, Ramos I, Lopes B, Valbon BF, Botteon C, et al. Astigmatic vector analysis of posterior corneal surface: a comparison among healthy, forme fruste, and overt keratoconic corneas. Am J Ophthalmol. 2016;167(7):65-71. http://dx.doi.org/10.1016/j.ajo.2016.04.008

4. Kunert KS, Russmann C, Blum M, Sluyterman G. Vector analysis of myopic astigmatism corrected by femtosecond refractive lenticule extraction. J Cataract Refract Surg. 2013;37(5):759-69. http://dx.doi.org/10.1016/j.jcrs.2012.11.033

5. Shamseer L, Moher D, Clarke M, Ghersi D, Liberati A, Petticrew M, Shekelle P, Stewart LA, the PRISMA-P Group. Preferred reporting items for systematic review and meta-analysis protocols (PRISMA-P) 2015: elaboration and explanation. BMJ. 2015;349:g7647. https://dx.doi.org/10.1136/bmj.g7647

6. Alpins N, Ong JK, Stamatelatos G. Corneal Topographic Astigmatism (CorT) to Quantify Total Corneal Astigmatism. J Refract Surg. 2015;31(3):182-6. http://dx.doi.org/10.3928/1081597X-20150224-02

7. Alpins N. A new method of analyzing vectors for changes in astigmatism. J Cataract Refract Surg. 1993;19(7):524-33. http://dx.doi.org/10.1016/S0886-3350(13)80617-7

8. Alpins N. New method of targeting vectors to treat astigmatism. J Cataract Refract Surg. 1997;23(1):65-75. http://dx.doi.org/10.1016/S0886-3350(97)80153-8

9. Alpins N. Vector analysis of astigmatism changes by flattening, steepening, and torque. J Cataract Refract Surg. 1997;23(12). http://dx.doi.org/10.1016/S0886-3350(97)80021-1

10. Alpins N. Treatment of irregular astigmatism. J Cataract Refract Surg. 1998;24(5):634-46. http://dx.doi.org/10.1016/S0886-3350(98)80258-7

11. Alpins N. Astigmatism analysis by the Alpins method. J Cataract Refract Surg. 2001;27(1):31 -49. http://dx.doi.org/10.1016/S0886-3350(00)00798-7

12. Piñero DP, Alió JL, Tomás J, Maldonado MJ, Teus MA, Barraquer RI. Vector Analysis of Evolutive Corneal Astigmatic Changes in Keratoconus. Invest Ophthalmol Vis Sci. 2011;52(7):4054-62. http://dx.doi.org/10.1167/iovs.10-6856

13. Thibos LN, Wheeler W, Horner D. Power vectors: an application of Fourier analysis to the description and statistical analysis of refractive error. Optom Vis Sci. 1997;74(6):367-75. http://dx.doi.org/10.1097/00006324-199706000-00019

14. Thibos LN, Horner D. Power vector analysis of the optical outcome of refractive surgery. J Cataract Refract Surg. 2001;27:80-5. http://dx.doi.org/10.1016/S0886-3350(00)00797-5

Giuliano de Oliveira Freitas
http://orcid.org/0000-0002-9348-1856
http://lattes.cnpq.br/2229984680546836

Renato Ambrósio Júnior
http://orcid.org/0000-0001-6919-4606
http://lattes.cnpq.br/1789497818458326

Milton Ruiz Alves
http://orcid.org/0000-0001-6759-5289
http://lattes.cnpq.br/6210321951145266

Received on: August 24, 2016.
Accepted on: September 14, 2016.